As further proof of my unsuitability to be a child minder (see
previous post) I found myself playing with an Ikea
LILLABO 20-piece basic set train.

The train set has 16 pieces of track (12 curves, two straight pieces and a two part bridge) and 4 pieces of train. What I wondered was... how many possible looping train tracks can be made using all 16 pieces?
The answer is... 9. Here's a picture of the 9 different layouts.
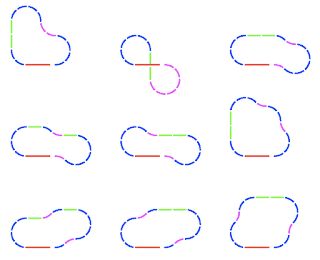
The picture was generated using a little program written in
Processing. The bridge is red, the straight pieces are green and the curves are blue or magenta depending on whether they are oriented clockwise or anticlockwise. The curved pieces can be oriented in either way.
To generate those layouts I wrote a small program which runs through all the possible layouts and determines which form a loop. The program eliminates duplicate layouts (such as those that are mirror images of each other).
It outputs a list of instructions for building loops. These instructions contain 15 characters C (clockwise curve), A (anticlockwise curve), S (straight piece) and B (the entire bridge). Here are the building instructions for all the shapes in the picture above:
AAAACCAAAASSAAB
CCCCCCSSAAAAAAB
CAAAAACASSAAAAB
CAAAAASCASAAAAB
CAAAAASSCAAAAAB
AAACAACAAASSAAB
ACAAAASACSAAAAB
ACAAAASSACAAAAB
AACAAASSAACAAAB
PS You can actually create more possible layouts than these because the Ikea pieces have a lot of play in them and can be abused to form other shapes. But where's the fun in that?
PPS Ikea can actually double the fun by adding just two more pieces. If they added two more curved pieces the number of possible tracks doubles to 18. If they added four curved pieces then the number of possible tracks goes to 130.
PPPS Here's the code
use strict;
use warnings;
# ----------------------------------------------------------------------------
# Program to determine all the possible valid closed loop train tracks
# possible using the Ikea Lillabo 20-piece basic train set (see
# http://www.ikea.com/gb/en/catalog/products/30064359). Note that
# although this is 20-piece there are only actually 16 pieces of track
# (the train itself is in four pieces).
#
# Written by John Graham-Cumming (http://www.jgc.org/)
#
# Released under the General Public License, version 2
#
# v1.0 - First public release
# ----------------------------------------------------------------------------
# Universal constant derived from 1 Kings 7:23 :-)
my $PI = 3.1415927;
# The length of a single straight piece. For the purposes of the
# program this is set at one but could be made into a real value if
# you wanted to output actual track lengths.
my $unit = 1;
# The number of curved pieces that make a full circle. Determined
# empirically. And the angle of the segment determined by a single
# curved piece in a circle.
my $curves_in_circle = 8;
my $radians_in_curve = 2 * $PI / $curves_in_circle;
# The 15 possible pieces: a straight edge (which has $unit length) and
# is used as the measurement for everything else, a bridge (which is
# twice the length of the straight edge; it is actually supplied in
# two pieces but for the purposes of this program is considered to be
# a single piece) and a curve (using $radians_in_curve above the
# length of the straight line between the ends of the curve is
# calculated).
#
# Each entry consists of three parts:
#
# length: the length in a straight line between the ends of the piece
# at its centre.
#
# angle: the angle (in radians) between the straight line through the
# piece and a tangent to the curve at the piece's start. This only
# applies to curved pieces where the straight line is the line joining
# its two endpoints.
#
# count: how many of these pieces are supplied.
#
# Note that curves can be placed in either a clockwise or
# anticlockwise direction. The program detects this by looking at the
# angle. If it's non-zero then the piece has two orientations.
my %pieces = (
Bridge => { length => $unit * 2,
angle => 0,
count => 1 },
Straight => { length => $unit,
angle => 0,
count => 2 },
# Here's a curved piece, the angle a is $radians_in_curve, the
# length l of a side is $unit. So length is the distance between
# the points labelled s and f. Bisect the angle a you get a right
# angle triangle with hypotenuse of length $unit and angle at the
# vertex of $radians_in_curve/2. So the angle b is $PI/2 -
# $radians_in_curve/2. By simple trigonometry the length is twice
# $unit * cos($PI/2-$radians_in_curve/2).
#
# s
# C
# . . C
# . b C
# l . . C
# . C
# . . C
# . a C
# . . . . . . . C
# o f
#
# To calculate the angle to the tangent at point s (the angle c),
# note that the angle formed by os and the tangent is a right angle
# (since os comes from the centre of the circle). So b+c is $PI/2
# but b is $PI/2 - $radians_in_curve/2 and so c is
# $radians_in_curve/2
#
# s
# .
# . . .
# . b c .
# l . . .
# . .
# . . .
# . a .
# . . . . . . . . . . .
# o f
#
Curve => { length => 2 * $unit * cos($PI/2-$radians_in_curve/2),
angle => $radians_in_curve/2,
count => 16 }
);
# This structure contains the position of the end of the current
# placed track (the X and Y coordinates) and the angle of the end of
# the piece of track in radians to the horizontal. Initially this is
# defined as location (0,0) and with an angle of 0.
#
# The goal will be to place pieces such that the cursor ends up at the
# %origin.
my %origin = (
angle => 0,
x => 0,
y => 0
);
# Some basic test tracks to make sure that the code does what I
# expect. This hash contains track layouts and the expected final
# position of the cursor for tests
my %tests = (
B => { x => 2 * $unit, y => 0, angle => 0 },
S => { x => $unit, y => 0, angle => 0 },
C => { x => 0.707, y => 0.293, angle => 0.785 },
A => { x => 0.707, y => -0.293, angle => -0.785 },
AA => { x => 1, y => -1, angle => -1.570 },
CC => { x => 1, y => 1, angle => 1.570 },
BSS => { x => 4 * $unit, y => 0, angle => 0 },
CCCC => { x => 0, y => 2 * $unit, angle => 0 },
AAAA => { x => 0, y => -2 * $unit, angle => -3.14 },
CCCCCCCC => \%origin,
CCCCCCCCCCCCCCCC => \%origin,
AAAAAAAA => \%origin,
AAAAAAAAAAAAAAAA => \%origin,
BCCCCCCSSAAAAAA => \%origin,
CCCCSCCCCS => \%origin,
CCCCACCACCCCACCA => \%origin
);
foreach my $t (sort keys %tests) {
my %ac = %origin;
my @as = split( '', $t );
build_track( \%ac, \@as );
if ( !cursor_match( \%ac, $tests{$t} ) ) {
die "Test $t failed: $ac{x} $ac{y} $ac{angle}\n";
}
}
# To avoid getting the same track in different directions we keep
# track of tracks that we've found for testing. The keys of this hash
# are the strings that describe the track layout (e.g. CCCCCCSSAAAAAA
# without the bridge piece).
my %found;
# Since there are only two interesting pieces of track (curve and
# straight) the algorithm for trying out all the combinations of
# pieces is broken into two parts. The outer loop runs through all
# combinations of curved pieces joined together with each piece
# getting to go clockwise or anticlockwise. This is done by
# generating all binary numbers between 0 and 2^12-1 (i.e. all 12 bit
# binary numbers) and using the bits to indicate whether a track piece
# goes clockwise (a 0) or anticlockwise (a 1).
#
# To avoid seeing the same track twice in symmetrical layouts the
# curved pieces are constrained to always finish with an anticlockwise
# piece. This is done by making the top bit in this loop be 0 by
# reducing the top number to 2^11-1
foreach my $curve (0..2**($pieces{Curve}{count}-1)-1) {
# Create an array containing the instructions for inserting
# pieces. The array is alpha and has entries B, C, A and S. A means
# add curved piece anticlockwise, S means add straight piece, C
# means a curved piece clockwise and B a bridge. This array will be
# fed into move_cursor to build the final track.
#
# The following piece of code uses the sprintf function to extract
# the bits from the $curve value into an array and then transform a
# 0 bit to A and a 1 bit to C.
my @instructions = map {$_?'C':'A'}
split( '', sprintf( "%0$pieces{Curve}{count}b", $curve ) );
# Then for each combination of curved pieces it's just a question of
# inserting the straight pieces in all possible positions. If there
# are 12 curved pieces then there are 13 possible places each
# straight piece can be inserted.
#
# To make it possible to modify the number of straight pieces the
# program doesn't assume that there are only two (which could just
# have been done with a pair of loops). So an array is initialized
# that will contain the positions of the n straight pieces and it is
# used to create the combinations.
#
# The initial position of the straight pieces is 0 and then 0
# (assuming just two) indicating that they are inserted before the
# first curved piece.
my @straight;
foreach my $i (0..$pieces{Straight}{count}-1) {
$straight[$i] = 0;
}
# Now run through all the possible valid straight positions and
# insert them into the curved positions
while (1) {
my @in = @instructions;
# Add the straight pieces to the list of 'instructions' at the
# appropriate places and then place the pieces. This creates a
# new array, @build, containing the track layout.
my @build;
my $s = 0;
my $c = 0;
while ( ( $s < $pieces{Straight}{count} ) ||
( $c < $pieces{Curve}{count} ) ) {
if ( $s < $pieces{Straight}{count} ) {
if ( $straight[$s] == $c ) {
push @build, ('S');
$s += 1;
next;
}
}
if ( $c < $pieces{Curve}{count} ) {
push @build, ($in[$c]);
$c += 1;
}
}
# Now add the bridge at end. Since there's only one bridge this
# simplification is made and it makes no difference to the outcome
# since all other combinations of straights and curves will be
# generated.
push @build, ('B');
my %cursor = %origin;
build_track( \%cursor, \@build );
# Finally see if this track layout results in a loop. The test
# for this is simple: is the last piece (represented by the
# %cursor) at the %origin position and orientation?
#
# If it matches in one direction then pop off the bridge, reverse
# the track, push back the bridge and try to rebuild. This will
# eliminate tracks that don't actually match up because the final
# piece approaches the bridge from the wrong direction.
if ( cursor_match( \%cursor, \%origin ) ) {
pop @build;
%cursor = %origin;
my $build1 = join('',@build);
@build = reverse @build;
my $build2 = join('',@build);
push @build, ('B');
my $build1a = $build1;
$build1a =~ tr [AC] [CA];
my $build2a = $build2;
$build2a =~ tr [AC] [CA];
if ( !exists( $found{$build1} ) ) {
build_track( \%cursor, \@build );
if ( cursor_match( \%cursor, \%origin ) ) {
my $build3 = undef;
if ( $build1 =~ /^(.*)SS(.*)$/ ) {
$build3 = join('',reverse split('',$1)) .
'SS' . join('',reverse split('',$2));
}
if ( !defined( $build3 ) ||
!exists( $found{$build3} ) ) {
print @build, "\n";
$found{$build1} = 1;
$found{$build2} = 1;
$found{$build1a} = 1;
$found{$build2a} = 1;
if ( defined( $build3 ) ) {
$found{$build3} = 1;
}
}
}
}
}
# Move the straight pieces to their next positions, this is where
# the while loop will exit once all the positions have been tried.
foreach my $i (0..$pieces{Straight}{count}-1) {
my $j = $pieces{Straight}{count}-1-$i;
if ( $straight[$j] < $pieces{Curve}{count} ) {
$straight[$j] += 1;
last;
} else {
$straight[$j] = -1;
}
}
foreach my $i (1..$pieces{Straight}{count}-1) {
if ( $straight[$i] == -1 ) {
$straight[$i] = $straight[$i-1];
}
}
my $terminate = 1;
foreach my $i (0..$pieces{Straight}{count}-1) {
if ( $straight[$i] != $pieces{Curve}{count} ) {
$terminate = 0;
last;
}
}
if ( $terminate ) {
last;
}
}
}
# Subroutine used to place a piece of track. It updates a %cursor
# hash passed to it
sub move_cursor
{
my ( $c, # Reference to the %cursor hash to be updated
$p, # Name of the piece be added
$h ) = @_; # Handedness for curved piece (1 or -1), omit if
# non-curved
if ( !defined( $h ) ) {
$h = 0;
}
$c->{x} += $pieces{$p}{length} * cos($c->{angle} +
$h * $pieces{$p}{angle});
$c->{y} += $pieces{$p}{length} * sin($c->{angle} +
$h * $pieces{$p}{angle});
if ( $h != 0 ) {
$c->{angle} += 2 * $h * $pieces{$p}{angle};
}
}
# Subroutine to build an entire track from a list of track pieces
# (with single character identifiers)
sub build_track
{
my ( $c, # Reference to the %cursor to update
$in ) = @_; # Reference to the list of build instructions
# This maps the characters in the @$in array into piece names and
# handedness (for the curved pieces). Note that direction is
# missing for the straight pieces and the undefined value is used in
# the following loop and passed to move_cursor for those
# pieces. move_cursor knows how to deal with this.
my %m = (
'A' => { piece => 'Curve', direction => -1 },
'B' => { piece => 'Bridge' },
'C' => { piece => 'Curve', direction => 1 },
'S' => { piece => 'Straight' } );
foreach my $i (@$in) {
move_cursor( $c, $m{$i}{piece}, $m{$i}{direction} );
}
}
# Determine whether two cursors represent the same position and
# orientation. Return 1 if so, 0 otherwise.
sub cursor_match
{
my ( $c, $d ) = @_; # References to two %cursor hashes
my $dx = round($$c{x}-$$d{x});
my $dy = round($$c{y}-$$d{y});
my $da = round(($$c{angle}-$$d{angle})/$PI);
$da -= int($da);
return ( ( $dx == 0 ) &&
( $dy == 0 ) &&
( $da == 0 ) );
}
# Perform rounding on a number to two decimal places
sub round
{
my ( $a ) = @_;
return int($a*100 + 0.5*($a <=> 0))/100;
}
PPPS Here's how I determined that a full circle was made up of eight curved pieces with a radius of one straight piece:
 Update
Update I received a message from Ikea about this:
Dear John
Thank you for sharing our passion for childrens products. It is very good for us to get input like this. I will forward your idea to the product developer who is responsible for our toys and maybe this improvements will be something for us to concider.
Thanks again for taking your time to give us feed back.
Best regards
Maria Thörn
Range manager childrens IKEA











