John Graham-Cumming's blog

Here's what he says: "I'm thinking of a number between 1 and 100. You can guess, after each guess I'll tell you whether high or low. You get it the first guess I'll give you five bucks. Four bucks, three, two, one, zero, you pay me a buck, you pay me two, you pay me three". 

The question is "Should you accept to play this game?". In the interview, Ballmer states that the answer is "No" for two reasons: firstly, because he can pick numbers that'll be the most difficult for you to determine, secondly because the expected value of the game (assuming Ballmer chooses randomly) is negative: you end up paying Ballmer.

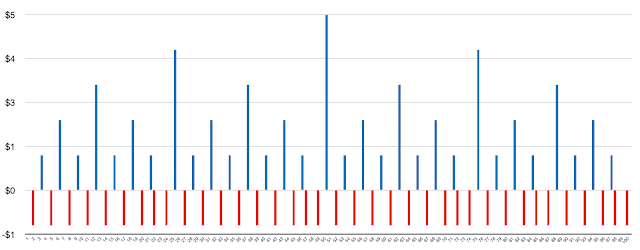
He's right on the first count. If you follow a binary search strategy (which will be optimal if he's choosing randomly) and he chooses one of 2, 5, 8, 11, 14, 17, 20, 22, 24, 27, 30, 33, 36, 39, 42, 45, 47, 49, 52, 55, 58, 61, 64, 67, 70, 72, 74, 77, 80, 83, 85, 87, 90, 93, 96, 98 or 100 then you owe him $1. For all other numbers you get $0 (if he chose 1, 4, 7, 10, 13, 16, 19, 23, 26, 29, 32, 35, 38, 41, 44, 48, 51, 54, 57, 60, 63, 66, 69, 73, 76, 79, 82, 86, 89, 92, 95 or 99) or a positive outcome (some of his money!).

In the video above Ballmer chooses 59 which a binary search strategy would have found in 5 steps resulting in the interviewer, Emily Chang, winning $1. She was actually pretty close to doing that. The binary search steps would be 50, 75, 62, 56, 59 and she guessed 50, 75, 60, 55, 57, 58, 59. 

On the second count (Baller implies the expected value is negative), if he's choosing randomly, then he's wrong. The expected value is $0.20 (calculated discretely using the code below). The code calculates the number of guesses for each value and an overall expected value assuming Ballmer chooses randomly.

use strict;
use warnings;

my @v = (0, 5, 4, 3, 2, 1, 0, -1, -2);

my $ev = 0;
my $ec = 0;

my @range = (1..100);

foreach my $r (@range) {
    my $l = $range[0];
    my $h = $range[$#range];

    my $s = 0;
    while (1) {
        $s += 1;
        my $g = int(($l + $h)/2);

        if ($r == $g) {
            print "$r found in $s steps (" . dollar($v[$s]) . ")\n";
            $ev += $v[$s];
            $ec += 1;
            last;
        }

        if ($g < $r) {
            $l = $g + 1;
            next;
        }

        if ($g > $r) {
            $h = $g - 1;
            next;
        }
    }
}

$ev /= $ec;
print "Game expected value is " . dollar($ev) . "\n";

sub dollar {

    my ($d) = @_;

    my $f = (int($d) == $d)?'%d':'%.2f';
    return sprintf("%s\$$f", ($d<0)?'-':'', abs($d));
}

This chart shows the expected winnings (or loss) depending on the number Ballmer chooses. The shape of the binary search can be seen in the chart itself.

A different way to think about the expected value and binary search is as follows:

1. On the first guess you choose 50 and win $5 with a probability of 1/100

2. On the second guess you choose 25 or 75 and win $4 with a probability of 2/100

3. On the third guess you choose 12, 37, 62 or 88 and win $3 with a probability of 4/100

4. On the fourth guess you choose 6, 18, 31, 43, 56, 68, 81 or 94 and win $2 with a probability of 8/100

5. And so on.

The gives the expected value as 5 * 1/100 + 4 * 2/100 + 3 * 4/100 + 2 * 8/100 + 1 * 16/100 + 0 * 32/100 + -1 * 37/100 (note the last term is the remaining possible numbers having reached the end of the binary search). That's 0.2.

Why was Ballmer wrong?

One possibility is that he didn't mean to have the $0 for 6 guesses. If he'd said "I'm thinking of a number between 1 and 100. You can guess, after each guess I'll tell you whether high or low. You get it the first guess I'll give you five bucks. Four bucks, three, two, one, you pay me a buck, you pay me two, you pay me three" then the expected value is -$0.49.

At work there's a little project to break up groups of employees into random groups (size 4) and set up Zoom calls between them. We're doing this to replace the serendipitous meetings that sometimes occur around coffee machines, in lunch lines or while waiting for the printer. And also, we just want people to get to know each other.

Which lead to me writing some code. The core of which is 'divide n elements into groups of at least size g minimizing the size of each group'. So, suppose an office has 15 employees in it then it would be divided into three groups of sizes 5, 5, 5; if an office had 16 employees it would be 4, 4, 4, 4; if it had 17 employees it would be 4, 4, 4, 5 and so on.

I initially wrote the following code (in Python):

    groups = [g] * (n//g)

    for e in range(0, n % g):
        groups[e % len(groups)] += 1

The first line creates n//g (// is integer division) entries of size g (for example, if g == 4 and n == 17 then groups == [4, 4, 4, 4]). The for loop deals with the 'left over' parts that don't divide exactly into groups of size g. If g == 4 and n == 17 then there will be one left over element to add to one of the existing [4, 4, 4, 4] groups resulting in [5, 4, 4, 4].

The e % len(groups) is needed because it's possible that there are more elements left over after dividing into equal sized groups than there are entries in groups. For example, if g == 4 and n == 11 then groups is initially set to [4, 4] with three left over elements that have to be distributed into just two entries in groups.

So, that code works and here's the output for various sizes of n (and g == 4):

    4 [4]
    5 [5]
    6 [6]
    7 [7]
    8 [4, 4]
    9 [5, 4]
    10 [5, 5]
    11 [6, 5]
    12 [4, 4, 4]
    13 [5, 4, 4]
    14 [5, 5, 4]
    15 [5, 5, 5]
    16 [4, 4, 4, 4]
    17 [5, 4, 4, 4]

But the code irritated me because I felt there must be a simple formula to work out how many elements should be in each group. After noodling on this problem I decided to do something that's often helpful... make the problem simple and naive, or at least, the solution simple and naive and so I wrote this code:

    groups = [0] * (n//g)

    for e in range(n):
        groups[e % len(groups)] += 1

This is a really simple implementation. I don't like it because it loops n times but it helps visualize something. Imagine that g == 4 and n == 17. This loop 'fills up' each entry in groups like this (each square is an entry in groups and numbers in the square are values of e for which that entry was incremented by the loop).

 

Can't remember that 9 x 7 is 63? Here's the really fast way to do it.

Lay your hands on the table and look at your fingers. Imagine they are numbered 1 to 10 from left to right. Find the 7th finger. There are 6 fingers to the left of it: that's the first digit of 9 x 7. There are three fingers to the right of it: that's the second digit. So the answer is 63.

Same thing works for the rest of the 9 times table (up to 9 x 10).

Here's a quick algebraic explanation of why that works. Suppose we're doing 9 x a where a is a number between 1 and 10. On your fingers you've got (a-1) fingers to the left of finger a and (10-a) fingers to the right. The result is 10 x (a-1) + (10-a) because the (a-1) is in the 10s position.

10 x (a-1) + (10-a)

= 10 x a - 10 + 10 - a

= 10 x a - a

= (10 - 1 ) x a

= 9 x a

Another thing you can spot this way is that the sum of the digits in the 9 times table is always 9. For example, 63 (6 + 3 = 9), 9 x 5 = 45 (4 + 5 = 9). Again, algebra shows why:

  (a-1) + (10-a)

= a - 1 + 10 - a

= 9

PS A reader writes that the 9 times table is also a palindrome (if you add a zero before 9 x 1): 09 18 27 36 45 54 63 72 81 90.

An interesting post on Hacker News shows tricks for dividing by 9. The fastest trick goes like this. Suppose you want to do 53876 / 9 in your head. You do the following:

1. The first digit is going to be the same as in the left hand side, so it's 5.

2. The second digit is the first digit plus the second digit: 5 + 3 = 8

3. The third digit is the previous answer plus the third digit: 8 + 8 = 16. Because that's bigger than 10 carry it to the digit above (which is now 9) and just take the rest. So it's 6.

4. The fourth digit is previous answer plus the fourth digit: 16 + 7 = 23. Again carry the tens to the preceding digit (which now becomes 8) and you're left with 3.

5. The last digit is the sum of all the digits: 23 + 6 = 29. For this final digit it's necessary to work out how many times 29 can be divided by 9 (it's 3). That gets added to the previous digit which becomes 6. The remainder (29 - 9 x 3 = 2) is the remainder of the whole calculation.

So, reading off the digits 53876 / 9 = 5986 remainder 2.

Why does this work? To show why I'll do a smaller example of a three digit number (with digits a, b, c) being divided by 9. The calculation abc/9 can be written as:

(a x 100 + b x 10 + c) / 9

=  a x 100 + b x 10 + c
   -------   ------   -
      9         9     9

=  a x (11 + 1/9) + b x (1 + 1/9) + c/9

=  a x 11 + b x 1 + (a + b + c)
                    -----------
                         9

=  a x 10 + a x 1 + b x 1 + (a + b + c)
                            -----------
                                 9

=  a x 10 + (a + b) + (a + b + c)
                      -----------
                           9

So, the first digit depends on a and any carry from (a + b), the second digit depends on (a + b) and any carry from the final term, and the only division left is the division of (a + b + c) by 9 and so that's where the remainder comes from.

Exactly the same pattern appears for longer numbers. Just be sure to carry; for very long numbers there could be a lot of carrying.

(Also fun, Squaring two digit numbers in your head.)

Some time ago I came across the trick that allows easy conversion of miles and kilometers (and also mph and km/h) using addition only. The trick uses the fact that the ratio of the Fibonacci numbers is very close to the conversion factor between miles and kilometers.

This is an example of turning multiplication to addition in a similar manner to the use of logarithms in a slide rule.

Firstly, the Fibonacci sequence is pretty easy to remember or regenerate from scratch because it is generated by the rule "the next number is the sum of the preceding two numbers". The sequence starts from 0 and 1 and then proceeds 1, 2, 3, 5, 8, 13, 21, 34, ... Each number is the sum of the previous two numbers.

Secondly, the ratio of consecutive Fibonacci numbers gets closer and closer to 1.62 the larger the numbers get. For example, 3/2 = 1.5, 8/5 = 1.6, 13/8 = 1.63, 21/13 = 1.62, 34/21 = 1.62, ...

Lastly, there are 1.61 kilometers in a mile. If you take the ratio of Fibonacci numbers as 1.62 then the error in using that for miles/kilometers conversions is about 0.5%. For everyday usage that's pretty good.

To go from kilometers (or kph) to miles (or mph) find the number in the list of Fibonacci numbers and look at the preceding number. For example, 34km (or kph) is 21.1 miles (or mph); using Fibonacci you get 21 miles (of mph). 8km is 4.97 miles; using Fibonacci it's 5 miles.

To go the other way (miles to kilometers) simply go the other way along the line. So find the number (in miles) in the Fibonacci sequence and get the kilometers from the next number.

On a recent trip to France I tried this out. The speed limit on a French autoroute is 130 kph which is 80.78 mph. Using the Fibonacci sequence it comes out at 80 mph (you can drop the 0 on both numbers since you're dealing with a ratio and go from 13 to 8 in the Fibonacci sequence).

When it's raining the speed limit drops to 110 kph. Now 11 doesn't appear in the sequence (again I've dropped the zero and will put it back in later). But 11 can be decomposed into 8 and 3 (11 = 8 + 3) and the answer obtained by looking at the mph figures for 11 and 3 in the Fibonacci sequence and adding them together. Thus we get 5 + 2 = 7 and so 110 kph is 70 mph (it's actually 68.35 mph). The error comes about because the early Fibonacci numbers are not quite at the right ratio. You can remove the error by remembering that 3 km is 1.8 (not 2) and then you get 5 + 1.8 = 6.8 (giving 68 mph).

Note that you can also use subtraction. For example, to work out 16 kilometers in miles you could look at 13 and 3 (to get 8 + 1.8 = 9.8) or you could do 21 and 5 (to get 13 - 3 = 10).

You can also play around with other tricks. For example, returning to 110 km you can see that it is 55 * 2 and 55 is a Fibonacci number. So at once you have 110km is 34 miles * 2 = 68 miles.

The children's game One Banana, Two Banana is a high stakes game of probability theory in action. Or something like that. Actually, it's a fun game where you have to take probability into account when deciding what to do.

Conceptually, the game is simple. There are 54 cards of five types. Three of the card types have bananas on them (one, two or three bananas), one card type has a banana skin on it and one card type has a swamp on it. All the cards are placed face down on the table and shuffled about. Each player takes turns at turning over as many cards as they want.

The total distance they move on the board (winning is a simple first past the post system) is the sum of the number of bananas on the banana cards. But if they pick a banana skin card then they stop picking cards and must reverse direction by the sum of the number of bananas on the banana cards. The swamp card simply stops a turn without a penalty.


There are six banana skin cards to start with and as they are removed from the pack they are placed on a special card for all to see. At every stage everyone knows the number of banana skin cards remaining. Thus you can adjust your strategy based on the number of banana skins that have caused others to go back.

So I wrote a little program that simulates One Banana, Two Banana games (or at least board positions) and see what the expected score is depending on the number of cards that the player chooses to pick. I assume a very simple strategy of deciding up front how many cards to pick. A more complexity strategy would be to look at the score as the player turns over cards and decide when to quit.

First, here's the code:

# Monte Carlo simulation of One Banana, Two Banana
#
# Copyright (c) 2010 John Graham-Cumming
#
# For game details see
#   http://www.amazon.co.uk/Orchard-Toys-One-Banana-Game/dp/B001T3AAI4
#
# In the game there are a total of 54 cards of five types:
# 
# 14 cards with three bananas on them
# 14 cards with two bananas on them
# 14 cards with one banana on them
# 6 cards with a swamp on them
# 6 cards with a banana skin
#
# The cards are placed face down on the table.  At each turn the
# player can take as many cards as they wish.  If they turn over a
# swamp or banana skin card they must stop; otherwise they stop when
# they choose.
#
# The total number of bananas is added up (call it X).  If the banana
# skin card was turned over then the player moves BACK X spaces, if
# not the player moves FORWARD X spaces.
#
# Players have perfect knowledge of the state of the cards as they are
# placed face up once drawn.  Once all six banana skin cards have be
# drawn the cards are all placed face down on the table again.

# The simulation runs through all the possible card positions and
# plays a large number of random draws for each possible number of
# cards a player might draw.  It then keeps track of the score for a
# number of different card counting scenarios.
#
# Card counting scenarios:
#
# Number of skins: the player only keeps track of the number of banana
# skins that are on the table.
#
# Number banana cards: the player calculates the number of banana
# cards on the table.
#
# Number of three bananas: the player keeps track of the number of
# high scoring three banana cards on the table.

use strict;
use warnings;

# This is a two dimensional array.  The first dimension is the number
# of skins (6, 5, 4, 3, 2, 1).  The second dimension is the number of
# cards the player will pick.  Each entry is a hash with keys score
# (the total score of all trials) and count (the total number of
# trials).

my @skins;

# Similar arrays to @skins, but here the first dimension is the number
# of cards on the table of the specific type.

my @bananas;
my @threes;

# Generate all possible valid board positions using nested loops.
# Note that the skin cards can never be zero because that's when the
# board resets.
#
# There are 6 x 7 x 15 x 15 x 15 possible board positions (115,248).

for my $sk (1..6) {
  for my $sw (0..6) {
    for my $on (0..14) {
      for my $tw (0..14) {
 for my $th (0..14) {

   # Arbitrarily chosen run of 100 plays

   for my $sim (0..99) {

     # Allow the player to pick up to 10 cards

     for my $to_pick (1..10) {

       # The state of the board at any time can be represented by
       # a 5-tuple (Skin, Swamp, One, Two, Three) giving the
       # number of cards of each type present on the playing
       # board.  The initial state is (6, 6, 14, 14, 14).

       my @cards = ( $sk, $sw, $on, $tw, $th );

       my $score = 0;
       for my $pick (1..$to_pick) {
  my $total = $cards[0] + $cards[1] + $cards[2] + $cards[3]
                         + $cards[4];
  my $picked = int(rand($total));
  if ( $picked < $cards[0] ) {
    $score = -$score;
    last;
  } elsif ( $picked < ( $cards[0] + $cards[1] ) ) {
    last;
  } elsif ( $picked < ( $cards[0] + $cards[1] + $cards[2] ) ) {
    $cards[2]--;
    $score += 1;
  } elsif ( $picked < ( $cards[0] + $cards[1] + $cards[2] +
          $cards[3] ) ) {
    $cards[3]--;
    $score += 2;
  } else {
    $cards[4]--;
    $score += 3;
  }
       }

       $skins[$sk][$to_pick]{score} += $score;
       $skins[$sk][$to_pick]{count}++;

       $bananas[$on+$tw+$th][$to_pick]{score} += $score;
       $bananas[$on+$tw+$th][$to_pick]{count}++;

       $threes[$th][$to_pick]{score} += $score;
       $threes[$th][$to_pick]{count}++;
     }
   }
 }
      }
    }
  }
  print "$sk\n";
}


if ( open F, ">skins.csv" ) {
  for my $i ( 1..6 ) {
    for my $k (1..10) {
      print F "$i,$k,$skins[$i][$k]{score},$skins[$i][$k]{count}\n";
    }
  }
  close F;
}

And here's a chart showing the average score from the Monte Carlo simulation for each of the six possible numbers of banana skins on the board. The X axis shows the number of cards picked (or desired to be picked), and the Y axis the average score.


If you look just at the maximum scores for each of the banana skin counts, then a simple pattern emerges.


So, just memorize that pattern and you'll be a better player. And also, if you are player and have exceeded the expected score with fewer than the recommended cards you'll know it's best to stop. I've removed that sentence because it is not correct. That's a different strategy based on stopping based on the cards you have already turned over; that deserves a separate analysis to find the best strategy.

Watch out Vegas, here I come.

I was staring at the checked pattern on the back of an airline seat the other day when I suddenly saw that the sum of the first n odd numbers is always a square. For example,

1
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16

And, of course, it occurred to me that it would be nice to be able to prove it. There are lots of ways to do that. Firstly, this is just the sum of an arithmetic progression starting at a = 1 with a difference of d = 2. So the standard formula gives us:

sum_odd(n) = n(2a + (n-1)d)/2
           = n(2 + (n-1)2)/2
           = n(1 + n - 1)
           = n^2

So, the sum of the first n odd numbers is n^2.

But using standard formulae is annoying, so how about trying a little induction.

sum_odd(1) = 1

sum_odd(n+1) = sum_odd(n) + (2n + 1)
             = n^2 + 2n + 1
             = (n+1)^2

But back to the airline seat. Here's what I saw (I added the numbering, Lufthansa isn't kind enough to do that for you :-):



The other thing I noticed was this:



You can view the square as the sum of two simpler progressions (the sum of the first n numbers and the sum of the first n-1 numbers):

1 + 3 + 5 + 7 =
1 + 2 + 3 + 4 +
    1 + 2 + 3

And given that we know from Gauss the sum of the first n numbers if n(n+1)/2 we can easily calculate:

sum_odd(n) = sum(n) + sum(n-1)
           = n(n+1)/2 + (n-1)n/2
           = (n^2 + n + n^2 - n)/2
           = n^2

What do you do on long flights?

A recent thread on Hacker News that I started with a flippant comment turned into a little mathematical puzzle.

What's the sum of the square of the first n whole numbers?

It's well known that the sum of the first n whole numbers is n(n+1)/2. But what's the value of sum(i=1..n) n^2? (I'll call this number S for the remainder of this post).

It turns out that it's easy to prove that S = n^3/3 + n^2/2 + n/6 by induction. But how is the formula derived? To help with reasoning here's a little picture of the first 4 squares stacked up one on top of the other:



If we fill in the blank squares to make a rectangle we have the basis of a derivation of the formula:



Looking at the formerly blank squares (that I've numbered to assist with the thinking) we can see that the columns have 1 then 1+2 then 1+2+3 and finally 1+2+3+4 squares. Thus the columns are sums of consecutive whole numbers (for which we already have the n(n+1)/2 formula.

Now the total rectangle is n+1 squares wide (in this case 5) and its height is the final sum of whole numbers up to n or n(n+1)/2 (in the image it's 4 x 5 / 2 = 10. So the total number of squares in the rectangle is (n+1)n(n+1)/2 (in the example that's 5 x 10 = 50).

So we can calculate S as the total rectangle minus the formerly blank squares which gives:

S  = (n+1)n(n+1)/2 - sum(i=1..n)sum(j=1..i) j
   = (n(n+1)^2)/2 - sum(i=1..n) i(i+1)/2
2S = n(n+1)^2 - sum(i=1..n) i(i+1)
   = n(n+1)^2 - sum(i=1..n) i^2 - sum(i=1..n) i
   = n(n+1)^2 - S - n(n+1)/2
3S = n(n+1)^2 - n(n+1)/2
   = n(n+1)( n+1 - 1/2 )
   = n(n+1)(n+1/2)
   = (n^2+n)(n+1/2)
   = n^3 + n^2/2 + n^2 + n/2
   = n^3 + 3n^2/2 + n/2
S  = n^3/3 + n^2/2 + n/6

In another forum I was just talking about a little technique that I came up with for securing a server that I want on the Internet, but to be hard for hackers to get into. I've done all the right things with firewalling and shutting down services so that only SSH is available. But that still leaves port 22 sitting there open for someone to bang on.

So what I wanted was something like port knocking (for an introduction to that you can read my DDJ article Practical Secure Port Knocking). To avoid doing the classic port knocking where you have to knock the right way to open port 22 I came up with a different scheme which I call Cryptographically and Constantly Changing Port Opening or C3PO.

The server and any SSH client who wish to connect to it share a common secret. In my case that's just a long passphrase that we both know. Both bits of software hash this secret with the current UTC time in minutes (using SHA256) to get 256 bits of random data. This data changes every minute.

The 256 bits gives me 16 words of random data. Those 16 words can be interpreted as 16 different port numbers. Once a minute the server reconfigures iptables to open those 16 ports forwarding one of them (which corresponds to word[0] in the hash) to SSH and the other 15 to a blacklist service.

At any one time 16 ports are open (i.e. respond to a SYN) with only one being SSH and the other 15 being a trap to be sprung by an attacker. The 16 ports change once a minute.

Since both sides can compute the hash the client is able to compute where the SSH server is residing at that moment and contact it. Once contact is established the connection remains open for the duration of the session. New sessions, of course, will need to recompute the hash once a minute.

The blacklist service serves to tarpit an attacker. Any connection attempt to one of the other 15 sockets causes the IP address of the attacker to be blacklisted (again an iptables change) which means that hitting any of the 15 ports causes the attacker to shut off their access to the SSH server for the next 15 minutes.

A casual NMAP of my machine gets your IP address blacklisted and shows up a random selection of open ports. A real user connects to the SSH server first time because they know where it resides.

Of course, this doesn't replace making sure that the SSH server is up to date, and that passwords are generated carefully, but it seriously frustrates a potential attacker.

If this is of interest to others I'd be happy to release my code (which is currently in Perl) as a GPL2 project.

Recently, I released C and Java versions of Steve Gibson's PPP system for password generation. Steve updated the algorithm to PPPv2 which uses a different hash (SHA256 instead of SHA384) and a slightly different plain text generation algorithm (see the PPP pages for details).

I've now updated my code to PPPv2 and am releasing it here.

The C source code is available in ppp-c.zip.

The Java source code is available in ppp-java.zip.

The compiled Java is available in ppp.jar.

Read my original blog posts for details. All source code is released under the BSD License.

I recently produced an open source implementation of Steve Gibson's Perfect Paper Passwords system in C. It occurred to me that a better implementation would be a Java client for my mobile phone (thus eliminating the need for printing and carrying the paper passwords).

Here's my PPP client implementation running on my Motorola RAZR. It's written in Java using CLDC 1.0 and MIDP 2.0.




You can download and install the JAR file. The current version is 1.0.0.

Steve Gibson has come up with a simple two-factor password scheme that relies on printed cards of passcodes generated using a combination of SHA-384 and Rijndael. The idea is that a system could prompt the user for one of the passcodes in addition to their normal password.

Steve calls this his Perfect Paper Passwords system and has given a detailed description of the algorithm.

As usual he's released code written in assembly language as a DLL for Windows. He hasn't released his source code (he never does), so I thought it would be interesting to write my own implementation of his algorithm. Here's the C code:

#include <sys/time.h>
#include <string.h>
#include <stdio.h>
#include <stdlib.h>

#include "rijndael.h"
#include "sha2.h"

#pragma pack(1)

typedef unsigned char Byte;

typedef union __Passcode {
  unsigned long as_long;
  struct {
    Byte byte[4];
  } bytes;
} Passcode;

typedef struct __PasscodeString {
  char character[5];
} PasscodeString;

typedef unsigned long long SixtyFour;

typedef union __OneTwoEight {
  struct {
    SixtyFour low;
    SixtyFour high;
  } sixtyfour;
  Byte byte[16];
} OneTwoEight;

typedef struct __SequenceKey {
  Byte byte[SHA384_DIGEST_SIZE];
} SequenceKey;

typedef unsigned long DWord;

const char * alphabet = "23456789!@#%+=:?abcdefghijkmnopqrstuvwxyzABCDEFGHJKLMNPRSTUVWXYZ";

void inc( OneTwoEight * i ) 
{
  ++i->sixtyfour.low;
  if ( i->sixtyfour.low == 0 ) {
    ++i->sixtyfour.high;
  }
}

void add( OneTwoEight * to, OneTwoEight * addend ) 
{
  SixtyFour low = to->sixtyfour.low;

  low += addend->sixtyfour.low;

  if ( ( low < to->sixtyfour.low ) || ( low < addend->sixtyfour.low ) ) {
    ++to->sixtyfour.high;
  }

  to->sixtyfour.low = low;
}

void ConvertPasscodeToString( PasscodeString * passcodeString,
         Passcode passcodeValue )
{
  Byte bytes[4];

  bytes[0] = passcodeValue.bytes.byte[0] & 0x3f;
  bytes[1] = ( ( passcodeValue.bytes.byte[0] & 0xc0 ) >> 6 ) +
    ( ( passcodeValue.bytes.byte[1] & 0x0f ) << 2 );
  bytes[2] = ( ( passcodeValue.bytes.byte[1] & 0xf0 ) >> 4 ) +
    ( ( passcodeValue.bytes.byte[2] & 0x03 ) << 4 );
  bytes[3] = ( ( passcodeValue.bytes.byte[2] & 0xfc ) >> 2 );

  int i;
  for ( i = 0; i < 4; ++i ) {
    passcodeString->character[i] = alphabet[bytes[i]];
  }

  passcodeString->character[4] = '\0';
}

void RetrievePasscodes( Passcode passcodeListBuffer[],
   OneTwoEight firstPasscodeNumber,
   int passcodeCount,
   SequenceKey * sequenceKey ) 
{
  int i;

#define KEY_BITS (int)256
  Byte key[KEYLENGTH(KEY_BITS)];

  for ( i = 0; i < KEYLENGTH(KEY_BITS); ++i ) {
    key[i] = sequenceKey->byte[i+16];
  }

  unsigned long rk[RKLENGTH(KEY_BITS)];
  OneTwoEight plain;

  for ( i = 0; i < 16; ++i ) {
    plain.byte[i] = sequenceKey->byte[i];
  }

  OneTwoEight block = firstPasscodeNumber;
  unsigned int skip = (unsigned int)(block.sixtyfour.low & 0xF);

  SixtyFour carry = block.sixtyfour.high & 0xF;
  block.sixtyfour.high >>= 4;
  block.sixtyfour.low >>= 4;
  block.sixtyfour.low |= (carry << 60);

  OneTwoEight temp = block;
  add( &block, &temp );
  add( &block, &temp );
  add( &plain, &block );

  int nrounds = rijndaelSetupEncrypt( rk, key, KEY_BITS );
  Byte cipher[16*3];

  int c = 0;

  while ( passcodeCount > 0 ) {
    rijndaelEncrypt( rk, nrounds, (Byte *)&plain.byte[0], &cipher[0] );
    inc( &plain );
    rijndaelEncrypt( rk, nrounds, (Byte *)&plain.byte[0], &cipher[16] );
    inc( &plain );
    rijndaelEncrypt( rk, nrounds, (Byte *)&plain.byte[0], &cipher[32] );
    inc( &plain );
    
    for ( i = skip; ( i < 16 ) && ( passcodeCount > 0 ); ++i ) {
      passcodeListBuffer[c].bytes.byte[0] = cipher[i*3];
      passcodeListBuffer[c].bytes.byte[1] = cipher[i*3+1];
      passcodeListBuffer[c].bytes.byte[2] = cipher[i*3+2];
      ++c;
      --passcodeCount;
    }

    skip = 0;
  }
}

void GenerateSequenceKeyFromString( char * string,
        SequenceKey * sequenceKey )
{
  sha384( (const unsigned char *)string, strlen( string ),
   (unsigned char *)sequenceKey );
}

void GenerateRandomSequenceKey( SequenceKey * sequenceKey ) {
  struct timeval t;
  gettimeofday( &t, 0 );

  char t_buffer[61];
  strftime( t_buffer, 60, "%c%d%e%H%I%j%m", localtime( &t.tv_sec ) );
  
  char msecs_buffer[32];
  sprintf( msecs_buffer, "%ld", t.tv_usec );

  char hostname_buffer[256];
  gethostname( hostname_buffer, 255 );

  char pointer_buffer[16];
  sprintf( pointer_buffer, "%p", sequenceKey );

  char loadavg_buffer[256];
  double samples[3];
  getloadavg( samples, 3 );
  sprintf( loadavg_buffer, "%f%f%f", samples[0], samples[1], samples[2] );

  char buffer[1024];
  sprintf( buffer, "%s-%s-%s-%s-%s", t_buffer, msecs_buffer, hostname_buffer,
    pointer_buffer, loadavg_buffer );

  GenerateSequenceKeyFromString( buffer, sequenceKey );
}

int ConvertHexToKey( char * hex, SequenceKey * key ) 
{
  int i, j;

  for ( i = 0, j = 0; i < 96; i += 2, ++j ) {
    char pair[3];
    sprintf( pair, "%c%c", hex[i], hex[i+1] );
    int x;
    sscanf( pair, "%x", &x );  
    key->byte[j] = (Byte)x;
  }
}

int main( int argc, char * argv[] )
{
  if ( argc == 1 ) {
    printf( "Error: You must provide the passphrase or sequence key as the first parameter\n" );
    return 1;
  }

  SequenceKey key;

  if ( strlen( argv[1] ) == 0 ) {
    printf( "Generating random sequence key\n" );
    GenerateRandomSequenceKey( &key );
  } else {
    if ( ( strlen( argv[1] ) == 96 ) && ( ConvertHexToKey( argv[1], &key ) ) ) {
      printf( "Using entered sequence key\n" );
    } else {
      printf( "Generating sequence key from passphrase\n" );
      GenerateSequenceKeyFromString( argv[1], &key );
    }
  }

  printf( "Sequence Key: " );
  int i;
  for ( i = 0; i < SHA384_DIGEST_SIZE; ++i ) {
    printf( "%2.2x", key.byte[i] );
  }
  printf( "\n" );

  if ( argc == 4 ) {
    OneTwoEight firstPasscode;
    
    // Warning! This only uses the bottom 64-bits of argv[2] and hence
    // can't convert a much higher number

    firstPasscode.sixtyfour.low = atoi( argv[2] );
    firstPasscode.sixtyfour.high = 0;

    int count = atoi( argv[3] );

    Passcode * pcl = malloc( sizeof( Passcode ) * count );

    RetrievePasscodes( pcl, firstPasscode, count, &key );

    for ( i = 0; i < count; ++i ) {
      PasscodeString str;
      ConvertPasscodeToString( &str, pcl[i] );
      printf( "%s ", &str.character[0] );
    }
    
    printf( "\n" );
  }

  return 0;
}

Now that's a little less flexible than all the options given in Steve's ppp.exe implementation, but it does compute the correct output and can easily be modified if you want your own implementation with source of PPP.

It uses this SHA-384 implementation and this Rijndael implementation.

Here's the output of my ppp program producing the first 70 passcodes:

$ ./ppp 53303f97ddcf91ed74391fc5c3661246
        32427e1c93c1a2e2836d006fa2653dc1
        fb94f8fbeefa5f1e9263c12878e0a95e 0 70
Using entered sequence key
Sequence Key: 53303f97ddcf91ed74391fc5c3661246
              32427e1c93c1a2e2836d006fa2653dc1
              fb94f8fbeefa5f1e9263c12878e0a95e 
VJNV gHoF PaRp T8FS tGw2 s%iT u7rp 
ZvN@ MWGb %574 ?DVF btRq PLTA DDtm 
C2TP Yin8 zMF@ a8%H zHvq Uwxc qkF7 
YuUk 8Ca? :ZvZ T9:? wki+ KiHq d?9b 
GY%5 !igR pc@p 3B@L eyVm 5PwY CAVs 
oKzK 43Mc nR%? i?@U oZUs Tbec xn6B 
9bVA UvJt DfAX =Gqp 7Abj M:6Y ENRs 
aXX= Eokx WjTj %MPV McSA GFTK XMdY 
49?Z Z?Hk G+A? zoK5 :Z8N z8NU WpM! 
=AB% RrSq %7:Y %=P8 RKXr di#5 4T3L 

Feel free to take my code and use it under the BSD license.